Résolution des sudoku
Un TIPE sur la résolution des sudoku à l'aide du langage Caml par deux méthodes, utilisant respectivement la logique et le backtracking.
- Parenté :
- Programmation
- Résolution des sudoku
Introduction
Dans le cadre d'un TIPE, je me suis intéressé à l'utilisation de l'informatique dans la résolution des grilles du jeu Sudoku.
Mes premiers essais dans l'écriture en Caml d'un algorithme destiné à compléter une grille donnée m'ont conduit à rédiger :
- d'une part un programme qui utilise un raisonnement logique à partir des données, comme le ferait un joueur humain,
- d'autre part une implémentation de la méthode du backtracking : il s'agit pour l'ordinateur de faire des hypothèses jusqu'à aboutir à une impossibilité, et dans ce cas à revenir sur ses pas pour tester l'hypothèse suivante, jusqu'à atteindre la dernière case de la grille.
J'ai d'abord travaillé seul sur le premier programme, dont le fonctionnement est issu de mon expérience du jeu. J'ai ensuite amélioré les méthodes de raisonnement logique après la lecture d'une publication scientifique de Narendra Jussien, de l'école des Mines de Nantes, qui présente des améliorations des techniques que j'utilisais.
Lors de l'utilisation de ce premier programme, j'ai été forcé de constater qu'il ne parvenait pas à résoudre certaines grilles. En effet, les grilles dites "démoniaques" nécessitent impérativement l'utilisation d'hypothèses. J'ai donc cherché un autre algorithme de résolution pour tenir compte de ces grilles. J'ai alors pensé à une méthode de type backtracking mais abandonné cette idée pensant que le temps d'exécution serait beaucoup trop long.
J'ai alors lu une remarque dans l'article Sudoku de Wikipédia qui précise que par backtracking, "une grille 9×9 est habituellement résolue en moins de trois secondes avec un ordinateur personnel moderne qui a recours à un interpréteur, et en quelques millisecondes avec un langage compilé". Étonné par ces valeurs, j'ai voulu les vérifier et j'ai finalement constaté qu'en effet, la résolution par backtracking traitait la plupart des grilles dans un temps inférieur à une seconde, sauf dans le cas des grilles très peu remplies où elle peut dépasser le quart d'heure.
J'ai donc rédigé un algorithme qui utilise successivement les deux méthodes afin de résoudre une grille le plus rapidement possible. En effet, on constate que la résolution par backtracking est bien plus rapide lorsque la grille est « optimisée » au préalable par l'algorithme logique, c'est-à-dire lorsque tous les nombres déductibles des données sont rajoutés dans la grille par cet algorithme.
Afin de tester mes deux programmes, j'ai téléchargé sur son site la banque de grilles de Gordon Royle, un chercheur australien qui collectionne les grilles de poids 17 (c'est-à-dire pour lesquelles 17 nombres sont donnés sur 81). J'ai choisi aléatoirement 5000 grilles sur les 40000 de la base et leur ai appliqué mes algorithmes. J'ai ainsi constaté que la résolution par la logique traitait 82% des grilles, avec un temps de résolution moyen de 117 millisecondes. Les 18% restants sont résolus par backtracking (après une optimisation par la logique) en 2,34 secondes en moyenne.
J'ai enfin étendu ces méthodes à toutes les grilles de côté carré (9×9, 16×16, 25×25...).
Présentation
|
Le Sudoku est un jeu bien connu dont le nom signifie « chiffre unique ». Il se joue habituellement avec des grilles de 9×9 cases dont certaines sont restées vides. Le but du jeu est de les remplir en tenant compte de la contrainte suivante : toutes les lignes, colonnes et régions doivent contenir une et une seule fois chacun des nombres de 1 à 9. Une grille possède par convention une unique solution. Ces grilles sont résolubles en utilisant une méthode particulière de raisonnement et/ou en faisant des hypothèses. Dans le cadre du TIPE, je me suis intéressé à toutes les grilles carrées dont le côté est lui-même un carré, c'est-à-dire aux grilles de 16×16, 25×25... cases. J'appellerai donc n la racine de ce nombre : ici n=3, 4, 5. Le nombre de case est alors : n4=81, 256, 625... J'appellerai enfin « région » les zones de cases sur et « zone » un ligne, colonne ou région. | 
|
Deux techniques de résolution
Raisonnement logique
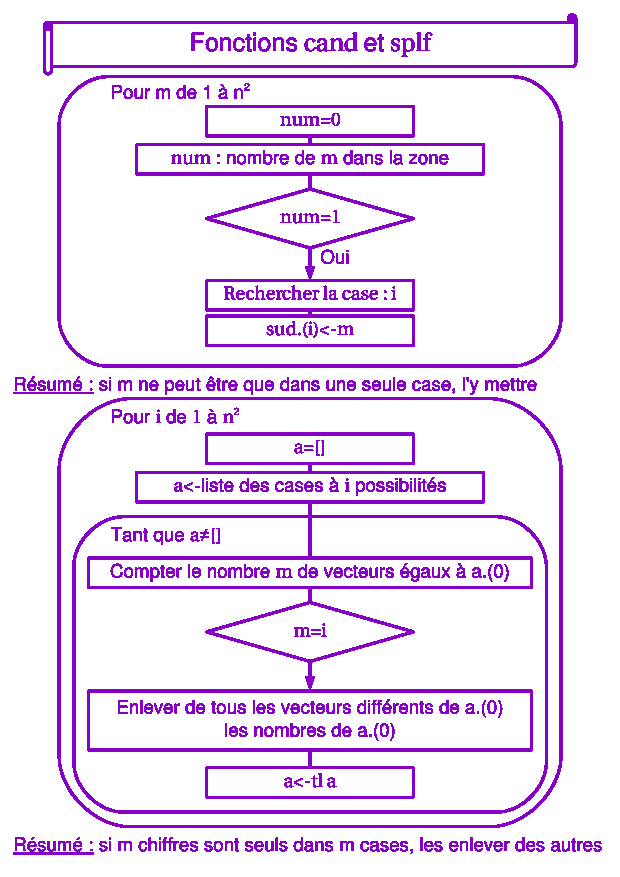
La première approche envisagée est celle par raisonnement logique, c'est-à-dire chercher quoi écrire dans une case en raisonnant sur des données. Cette technique comporte elle-même deux approches : la recherche des intrus et celle des candidats, expliqués sur ce schéma.
Recherche des intrus
Comme son nom l'indique, cette recherche vise à éliminer les nombres ne pouvant pas être inscrits dans la case étudiée. Il s'agit donc des nombres déjà présents dans la même zone. Lorsqu'il n'y a plus qu'un seul nombre possible, la case est remplie.
Recherche des candidats
Ici, au contraire, on regardera quels sont les nombres ne pouvant se placer que dans cette case de la zone. Si l'on trouve un tel nombre, il est alors certain et on l'inscrit dans la seule case possible.

Amélioration
On peut améliorer cette méthode assez simplement : si l'on trouve plusieurs positions possibles pour un même nombre dans une même zone et que toutes ces positions se trouvent dans l'intersection de cette zone avec une seconde zone, alors on peut enlever ce nombre de la liste des possibilités de toutes les autres cases de la seconde zone.
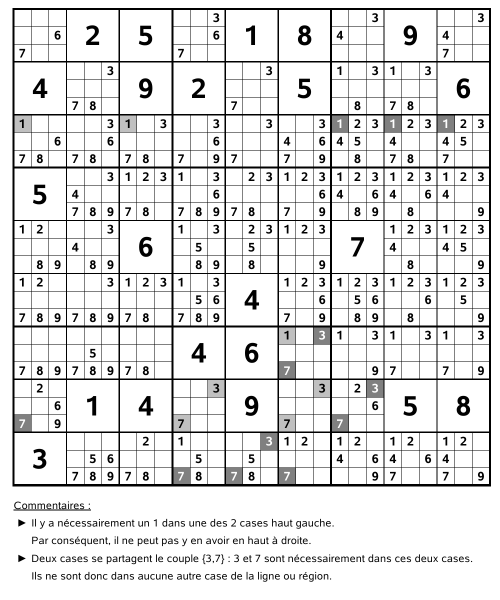
Méthode des simplifications
Il s'agit d'une amélioration de la recherche des intrus. En effet, cette méthode consiste à rechercher cases appartenant à la même zone et partageant nombres possibles. Ces nombre s'écrivent nécessairement dans ces cases et donc dans aucune autre case de la zone.
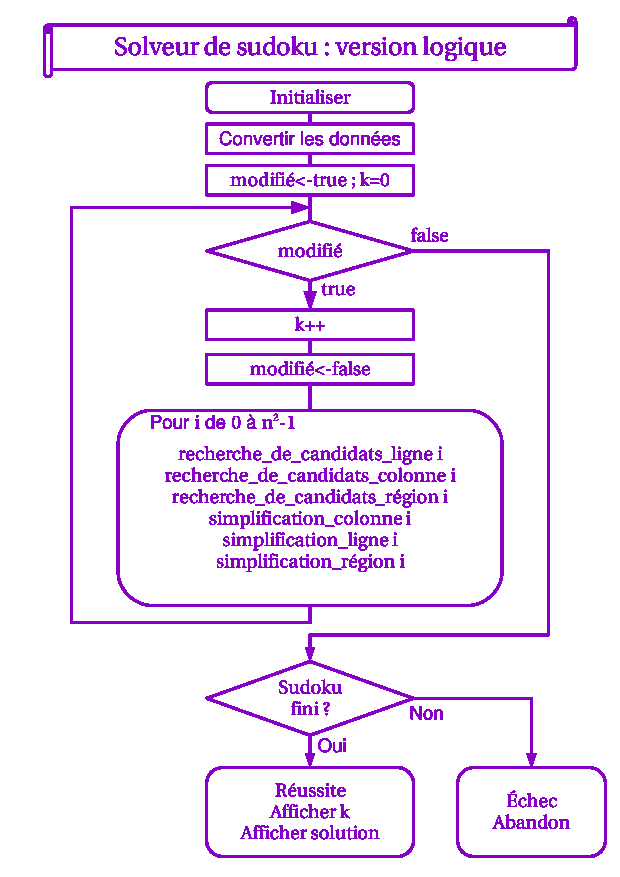
On en déduit l'algorithme de résolution par la logique, présenté sur le schéma.
Hypothèses et backtracking
Principe
Cette seconde technique consiste à supposer que la valeur d'une case est un certain nombre et à faire de même pour toutes les cases suivantes jusqu'à rencontrer une impossibilité. On recule alors autant que nécessaire en incrémentant les valeurs des cases, et ce jusqu'à remplir la grille. Cette méthode est appelée « backtracking ».
Algorithme
On en déduit l'algorithme de résolution par backtracking, présenté sur le schéma.
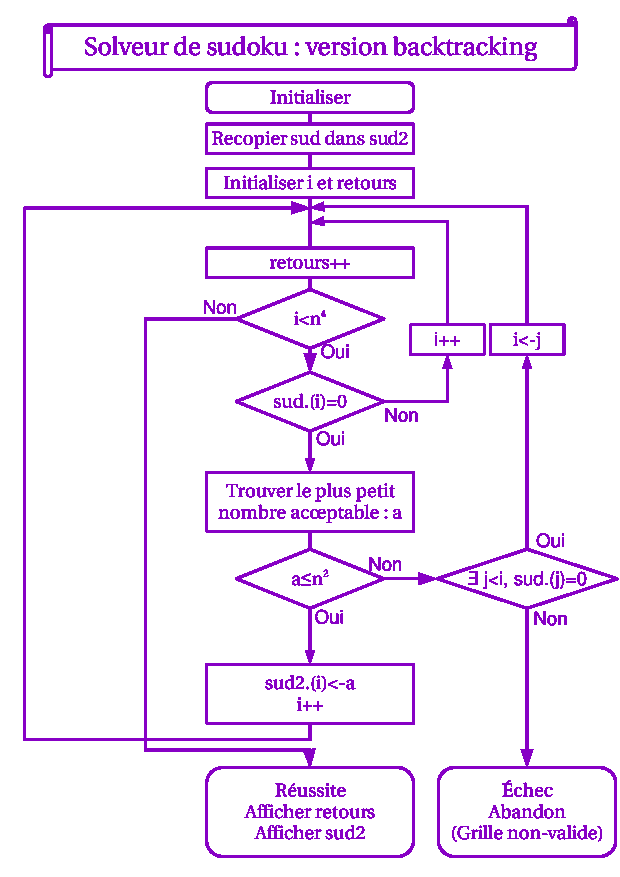
Explications
Notes à propos de ce schéma logique :
- La variable "retours" ne sert à rien d'autre qu'à compter combien de retours en arrière ont été nécessaires pour résoudre la grille. Elle n'est pas utile à la résolution de la grille mais fournit des statistiques sur les grilles.
- La variable J désigne l'indice d'une case vide dans la grille initiale (sud) et située "avant" la case en cours (J<I). C'est vers sud(J) que l'on va "reculer" (I<-J) si l'on ne trouve pas de solution lors du traitement de la case sud(I). En effet, reculer d'une case ne suffirait pas, puisque l'on pourrait tomber sur une case initialement remplie (et alors l'algorithme reprendrait dans le bon sens, c'est-à-dire par I++ soit le I précédent).
Implémentation
J'ai donc implémenté ces algorithmes dans le langage CAML. Sont donnés ci-dessous les code-sources ainsi que des sorties de l'exécution à l'écran et les historiques des versions.
Programme logique
Voici le code source :
(*
Programme logique de résolution des sudoku de taille n*n
Auteur : Peter Potrowl
Origine : www.sitemai.eu
Numéro de version : 1.10
*)
let sudoku data = (*sdk normal : n=3,n2=9,n4=81 *)
let n4=vect_length data in
let n=int_of_float (sqrt (sqrt (float_of_int n4))) in
let n2=n*n in
let init=make_vect n2 0 in for i=0 to n2-1 do init.(i)<-i+1 done;
let sud=make_vect n4 init in (*initialise la grille de n2.n2.n2 *)
let modif = ref true in
let region r = (*renvoie la liste des cases de la région r*)
let res=make_vect n2 0 in
for i=0 to n-1 do for j=0 to n-1 do
res.(i*n+j)<-((r-(r mod n))*n2+n*(r mod n)+j+n2*i);done;done;res in
let search v c = try (*recherche la valeur v dans la case c*)
for i=0 to (vect_length (sud.(c)))-1 do
if (sud.(c)).(i) = v then raise Exit;done;
false with Exit -> true in
let enleve v c = (*enlève la valeur v à la case c*)
if search v c then begin
let m=(vect_length (sud.(c)))-1 in
let res = make_vect m 0 and k=ref 0 in
for i=0 to m do if (sud.(c)).(i) <> v
then (res.(!k)<-(sud.(c)).(i);incr k) done;
sud.(c)<-res;modif:=true;end in
let affecte v c = (*affecte la valeur v à la case c*)
if vect_length (sud.(c)) <> 1 then (sud.(c)<-[|v|];modif:=true) in
let display sud = (*affiche la grille*)
for i=0 to n4-1 do if i mod n2 = 0 then print_newline();
if vect_length (sud.(i)) = 1 then
(if (sud.(i)).(0)<10 && n2>10 then
print_string " ";print_int (sud.(i)).(0);print_string " ")
else (if n2>10 then print_string " ";print_string ("0 "));done;
print_string "\n\n" in
let cand_lig l = (*recherche candidat dans une ligne*)
for m=1 to n2 do let temp=ref [] and r=ref [] in
for i=0 to n2-1 do if search m (l*n2+i) then
(temp:=(l*n2+i)::(!temp);r:=union !r [(i/n+n*(l/n))];);done;
if list_length !temp=1 then affecte m (hd !temp)
else begin if (list_length !r)=1 then
begin let reg=region (hd !r) in
for k=0 to n2-1 do
if (reg.(k)<l*n2 || reg.(k)>=(l+1)*n2)
then enleve m reg.(k);
done;end;end;
done; in
let cand_col c = (*recherche candidat dans une colonne*)
for m=1 to n2 do let temp=ref [] and r=ref [] in
for i=0 to n2-1 do if search m (i*n2+c) then
(temp:=(i*n2+c)::(!temp);r:=union !r [((c/n)+n*(i/n))];); done;
if list_length !temp=1 then affecte m (hd !temp)
else begin if (list_length !r)=1 then
begin let reg=region (hd !r) in
for k=0 to n2-1 do
if reg.(k) mod n2 <>c then enleve m reg.(k);
done;end;end;
done in
let cand_reg r = (*recherche candidat dans une région*)
let reg=region r in
for m=1 to n2 do let num=ref 0 and l=ref [] and c=ref [] in
for i=0 to n2-1 do if search m reg.(i) then
(incr num;l:=union !l [reg.(i)/n2];
c:=union !c [reg.(i) mod n2]) done;
if !num=1 then affecte m ((hd !l)*n2+(hd !c)) else begin
if (list_length !l)=1 then begin for k=0 to n2-1 do
if k/n+n*((hd !l)/n)<>r then enleve m ((hd !l)*n2+k);done;end;
if (list_length !c)=1 then begin for k=0 to n2-1 do
if (hd !c)/n+n*(k/n)<>r then enleve m (k*n2+(hd !c));done;end;end;
done in
let splf_lig l = (*simplifie les possibilités de la ligne l*)
for i=0 to n2-1 do let a=ref [(l*n2+i)] in
for j=i+1 to n2-1 do if sud.(l*n2+i)=sud.(l*n2+j) then
a:=(l*n2+j)::(!a);done;
if list_length !a=vect_length sud.(l*n2+i) then
for k=0 to n2-1 do if not (mem (l*n2+k) (!a)) then
for m=0 to vect_length sud.(l*n2+i)-1 do
enleve sud.(l*n2+i).(m) (l*n2+k) done;
done;done;in
let splf_col c = (*simplifie les possibilités de la colonne c*)
for i=0 to n2-1 do let a=ref [(i*n2+c)] in
for j=i+1 to n2-1 do if sud.(i*n2+c)=sud.(j*n2+c) then
a:=(j*n2+c)::(!a);done;
if list_length !a=vect_length sud.(i*n2+c) then
for k=0 to n2-1 do if not (mem (k*n2+c) (!a)) then
for m=0 to vect_length sud.(i*n2+c)-1 do
enleve sud.(i*n2+c).(m) (k*n2+c) done;
done;done;in
let splf_reg r = (*simplifie les possibilités de la région r*)
let reg=region r in
for i=0 to n2-1 do let a=ref [reg.(i)] in
for j=i+1 to n2-1 do if sud.(reg.(i))=sud.(reg.(j)) then
a:=(reg.(j))::(!a);done;
if list_length !a=vect_length sud.(reg.(i)) then
for k=0 to n2-1 do if not (mem (reg.(k)) (!a)) then
for m=0 to vect_length sud.(reg.(i))-1 do
enleve sud.(reg.(i)).(m) (reg.(k)) done;
done;done;in
let fait sud = (*dit si le sudoku est fini ou non*)
let res=ref true in for i=0 to n4-1 do
if vect_length (sud.(i)) <> 1 then res:=false done;!res in
(*on entre données dans grille :*)
for i=0 to n4-1 do if data.(i) <> 0 then sud.(i)<-[|data.(i)|];done;
print_string "\nRésolution du Sudoku suivant :\n";display sud;
let k=ref 0 in print_string "Compteur d'itérations : ";
while !modif do print_int !k;print_string " ";modif:=false;
for i=0 to n2-1 do
(cand_lig i;cand_col i;cand_reg i;splf_col i;splf_lig i;splf_reg i)
done;
incr k;done;
if fait sud then print_string "\n\nLa solution est :\n"
else print_string "\n\nSudoku non résolu !\n";display sud;;
Et voici un exemple d'exécution sur des données de taille 3 :
sudoku : int vect -> unit = <fun> # sudoku [| 7;6;0;0;0;2;5;0;0; 9;0;0;7;5;0;0;0;3; 0;0;0;0;0;6;9;0;0; 0;0;4;0;1;0;0;0;9; 0;8;0;0;0;0;0;5;0; 3;0;0;0;8;0;4;0;0; 0;0;2;3;0;0;0;0;0; 8;0;0;0;2;1;0;0;4; 0;0;6;5;0;0;0;3;8 |];; Résolution du Sudoku suivant : 7 6 0 0 0 2 5 0 0 9 0 0 7 5 0 0 0 3 0 0 0 0 0 6 9 0 0 0 0 4 0 1 0 0 0 9 0 8 0 0 0 0 0 5 0 3 0 0 0 8 0 4 0 0 0 0 2 3 0 0 0 0 0 8 0 0 0 2 1 0 0 4 0 0 6 5 0 0 0 3 8 Compteur d'itérations : 0 1 2 3 4 5 6 La solution est : 7 6 3 8 9 2 5 4 1 9 2 1 7 5 4 8 6 3 5 4 8 1 3 6 9 7 2 6 5 4 2 1 7 3 8 9 2 8 9 4 6 3 1 5 7 3 1 7 9 8 5 4 2 6 4 9 2 3 7 8 6 1 5 8 3 5 6 2 1 7 9 4 1 7 6 5 4 9 2 3 8 - : unit = ()
Historique des versions :
Historique des versions : * 1.01 : Version de base avec recherche des intrus et des candidats * 1.02 : Changement de structure : une fonction et des sous-fonctions * 1.03 : Support des grilles de toutes tailles : (3,9,81)->(n,n2,n4) * 1.04 : Amélioration de l'efficacité de la technique de résolution * 1.05 : Ajout de la méthode des simplifications * 1.06 : Allègement du code source et meilleure complexité * 1.07 : Allègement du code source et meilleure complexité * 1.08 : Nouvelle recherche des candidats, avec intersections de zones * 1.09 : Meilleure complexité pour la recherche des candidats * 1.10 : Allègement de la méthode des simplifications
Programme de Backtracking
Voici le code source :
(* Programme de backtracking de résolution des sudoku de taille n*n Auteur : Peter Potrowl Origine : www.sitemai.eu Numéro de version : 1.3 *) let sudoku sud = let n4=vect_length sud in let n=int_of_float (sqrt (sqrt (float_of_int n4))) in let n2=n*n in let sud2=make_vect n4 0 in (*initialise la grille solution de n2.n2 *) let possible m c = (*est-il possible de mettre m en c ?*) let l=c/n2 and col = c mod n2 in let reg = col/n + (l/n)*n in try for i=(c/n2)*n2 to (c/n2)*n2+(n2-1) do if sud2.(i)=m then raise Exit done; (*ligne*) for i=0 to n2-1 do if sud2.(col+n2*i)=m then raise Exit done; (*colonne*) for i=0 to n-1 do for j=0 to n-1 do if sud2.((reg-(reg mod n))*n2+(reg mod n)*n+j+(n2*i))=m then raise Exit done done;(*region*) true with Exit -> false;in for i=0 to n4-1 do sud2.(i)<-sud.(i) done; (*recopie la grille*) let i = ref 0 and t=ref 0 in while !i<n4 do begin if sud.(!i)=0 then begin (* v donne le premier nombre acceptable supérieur à la valeur courante :*) let a=ref (sud2.(!i)+1) in while not (possible !a !i) && !a<=n2 do incr a done; if !a<=n2 then (sud2.(!i)<-(!a);incr i) else if !i>0 then (sud2.(!i)<-0;decr i;incr t; while !i<n4 && sud.(!i)>0 do decr i;if !i<0 then i:=n4;done;) (* détermine la première case vide avant la case courante ^ *) else i:=n4 (* si aucune possibilité pour la 1è case, abandon *) end else incr i;end;done; print_string "\nCompteur d'itérations : ";print_int !t;print_newline(); for i=0 to n4-1 do if i mod n2 = 0 then print_newline(); if sud2.(i)<10 && n2>10 then print_string " "; print_int sud2.(i);print_string " ";done;print_newline();;
Et voici un exemple d'exécution sur des données de taille 4 :
sudoku : int vect -> unit = <fun> # sudoku [| 15; 0;13;14; 0; 1;16; 7;10; 8;11; 0; 5; 2; 0; 6; 2; 0; 3;12;10; 0; 0; 4; 6; 0; 0; 7;14;15; 0;11; 8;11; 7; 0; 2; 0; 0; 0; 0; 0; 0; 4; 0;13; 1;10; 10;16; 1; 9; 0;15; 0; 6;12; 0;14; 0; 7; 3; 4; 8; 0;13; 0; 3; 0; 4; 0;16;15; 0; 2; 0; 8; 0; 6; 0; 0; 0; 0; 0; 0;14; 0; 0; 0; 0; 4; 0; 0; 0; 0; 0; 7; 6; 0; 2; 0; 0; 9; 1;13;11; 0; 0; 4; 0; 5;15; 1;12; 4; 0; 0; 0; 0;15;16; 0; 0; 0; 0; 7; 3;13; 6; 3;12; 0; 0; 0; 0;10; 2; 0; 0; 0; 0; 8;14; 1; 11; 9; 0; 4; 0; 0; 7; 5; 8; 1; 0; 0;13; 0; 2; 3; 0; 0; 0; 0; 0; 8; 0; 0; 0; 0; 7; 0; 0; 0; 0; 0; 0; 8; 0;15; 0; 2; 0;11; 4; 0;12; 0; 6; 0; 7; 0; 3; 1;11;10; 0; 9; 0; 8;14; 0; 5; 0; 2;12;13; 7; 9;15; 6; 0;13; 0; 0; 0; 0; 0; 0; 8; 0; 4;11;14; 12; 0; 8;16;14; 0; 0; 3; 9; 0; 0; 2; 1; 6; 0; 5; 4; 0; 2;13; 0; 7; 5;12;11; 3; 6; 0; 9;10; 0;16 |];; Compteur d'itérations : 94638 15 4 13 14 3 1 16 7 10 8 11 9 5 2 12 6 2 5 3 12 10 13 8 4 6 16 1 7 14 15 9 11 8 11 7 6 2 12 14 9 5 15 3 4 16 13 1 10 10 16 1 9 5 15 11 6 12 2 14 13 7 3 4 8 14 13 9 3 11 4 10 16 15 7 2 5 8 1 6 12 5 10 15 8 7 14 12 13 1 6 4 3 11 9 16 2 7 6 16 2 8 3 9 1 13 11 10 12 4 14 5 15 1 12 4 11 6 5 2 15 16 9 8 14 10 7 3 13 6 3 12 7 4 16 13 10 2 5 9 11 15 8 14 1 11 9 14 4 12 6 7 5 8 1 15 10 13 16 2 3 16 2 5 1 9 8 15 14 3 13 7 6 12 11 10 4 13 8 10 15 1 2 3 11 4 14 12 16 6 5 7 9 3 1 11 10 16 9 6 8 14 4 5 15 2 12 13 7 9 15 6 5 13 10 1 2 7 12 16 8 3 4 11 14 12 7 8 16 14 11 4 3 9 10 13 2 1 6 15 5 4 14 2 13 15 7 5 12 11 3 6 1 9 10 8 16 - : unit = ()
Historique des versions :
Historique des versions : * 1.1 : Version de base * 1.2 : Réduction du code à une seule fonction * 1.3 : Support des grilles de taille n quelconque
Constat
Les grilles proposées dans la presse sont souvent classées par difficulté. On peut constater que les 2 algorithmes fonctionnent indépendamment pour les grilles « faciles », « moyennes », « difficiles » mais que seul le backtracking fonctionne sur certaines grilles dites « démoniaques », car celles-ci nécessitent absolument de faire des hypothèses.
Complexité et statistiques
Complexité spatiale
La complexité spatiale est très simple à calculer.
Programme logique
Pour le programme logique, les seules données stockées en mémoire sont dans une grille de n4 cases dont chacune contient un vecteur de taille n2. Au total, la complexité spatiale est en n6 et elle diminue au cours du temps car le nombre de possibilités décroît.
Programme de backtracking
Pour le programme de backtracking, deux grilles de taille n4 sont stockées en mémoire, donc la complexité spatiale est en n4.
Complexité temporelle
C'est cette complexité qui fait le lien avec le thème « le temps » de cette année (2007).
J'ai calculé la complexité temporelle de chacun des deux algorithmes.
Je trouve :
- une complexité en O(n11) pour le programme logique.
- une complexité en O(en×ln(n)) pour celui de backtracking.
Programme logique
Pour évaluer cette complexité, il convient l'évaluer celles de toutes les sous-fonctions puis l'utilisation de ces sous-fonctions par le programme lui-même.
On crée d'abord 5 sous-fonctions simples, en particuliers celle de recherche d'un nombre dans les possibilités d'une case, en O(n2) et celle qui enlève un tel nombre d'une case, de même complexité.
Il est alors facile d'évaluer la complexité des fonctions de recherche de candidats : celles-ci testent les n2 nombres possibles en lançant la fonction recherche dans les n2 cases de la zone : la complexité est donc en O(n6). L'amélioration proposée de change que la constante devant ce O
De même, on évalue la complexité des fonctions de simplification des possibilités. On obtient cette fois-ci une majoration en O(n8).
Étant donné que ces fonctions sont appelées n2 fois à chaque itération et que l'on estime à un O(n) le nombre d'itérations, on obtient un O(n11) pour la complexité du programme.
Programme de backtracking
Il est assez difficile d'estimer la complexité de cet algorithme. En effet, ce programme utilise une fonction externe qui indique si un nombre donné peut être placé dans une case donnée, en fonction des autres nombres de la grille. Elle a une complexité en O(n2). Mais combien de fois est-elle appelée lors d'une exécution ?
On peut représenter l'action d'un programme de backtracking comme l'exploration en profondeur d'un arbre. Ici, il est clair qu'explorer tout l'arbre se fait en O(n2n4) opérations. Cependant, si d est le nombre de cases déjà remplies, on a un O(n2n4-d). On peut alors faire plusieurs remarques :
- à n constant, la constante devant le O diminue beaucoup avec le nombre de données. Ainsi, par exemple, la grille donnée à l'une des finales de la coupe du monde de sudoku nécessite plus de 6 minutes d'exécution et plus de 5 millions de retours en arrière pour trouver son unique solution. Elle est de poids 17 et O(n2n4-d)=1,5×1069. On peut l'optimiser avec le programme de logique : celui-ci ne parvient pas à la résoudre mais trouve 5 nombres certains et ainsi augmente le poids de la grille à 21. L'exécution du backtracking ne nécessite alors plus que 2 minutes et 1,5 millions de retours en arrière. On a alors O(n2n4-d)=1,9×1067
D'où l'idée de créer un troisième programme, qui se présente comme une combinaison des deux précédents et qui cherche à déterminer un maximum de nombres avant de finir la résolution par backtracking. - D'autre part, si l'on estime à 25 % le nombre de données d'une grille, en général, on peut écrire d=n4 et donc T2(n)=O(n1,5n4) et donc T2(n)=O(en×ln(n)).
Statistiques
Afin de comparer l'efficacité de ces deux algorithmes, j'ai voulu les tester sur un grand nombre de grilles, et les plus difficile possibles. Or, le chercheur australien Gordon Royle possède une collection de plus de 40000 grilles de poids 17, c'est-à-dire dont 17 nombres sur 81 sont donnés. Ces grilles font partie des plus difficiles connues à ce jour. La collection est disponible sur son site web, sous la forme d'un fichier texte.
J'ai donc choisi 5000 grilles au hasard dans cette liste et j'ai pu en tirer les conclusions suivantes :
- le programme logique est venu à bout de 4143 grilles, soit 82,86 % avec un temps total de résolution de 8 minutes et 7 secondes soit en moyenne 117 ms par grille (!).
- le programme de backtracking sait résoudre 100% des grilles mais en l'exécutant sur une grille de poids 17, la résolution peut prendre plus d'un quart d'heure pour une seule grille !
D'où l'idée d'un troisième algorithme qui combine les deux précédents : cet algorithme, en raisonnant par la logique, découvre le plus possible de nombres certains dans la grille avant que les derniers nombres inconnus ne soient découverts par backtracking. Cette « optimisation par la logique » permet d'augmenter le poids des grilles. Ainsi, les 857 grilles de poids 17 non-résolues par la logique ont pu être optimisées et le poids moyen obtenu est de 47,63, c'est-à-dire qu'en moyenne, près de 59% de la grille peut-être remplie par la logique.
Après cette étape, l'exécution de l'algorithme de backtracking est bien plus rapide puisque le temps de résolution passe de plus 15 minutes à seulement 2,34 secondes.
Finalement, ce troisième algorithme a un temps moyen de résolution de 0,5 secondes par grille, ce qui est plutôt raisonnable pour des grilles de poids 17. En effet, Gary McGuire a démontré en janvier 2012 qu'il n'existait pas de grille de poids inférieur à 17 à solution unique et par conséquent, les grilles de Gordon Royle sont parmi les plus difficiles au monde.
Méthode de travail et problèmes rencontrés
J'ai commencé par programmer l'algorithme de raisonnement logique avec seulement la recherche des intrus, et ce sur des grilles classiques . Après l'avoir testé sur quelques grilles, j'ai constaté qu'il fonctionnait sur les grilles « faciles » et « moyennes » mais n'était pas suffisant pour les grilles « difficiles ». J'ai donc du rajouter la recherche par candidats. L'algorithme pouvait alors résoudre les trois difficultés.
J'ai ensuite lu sur Internet qu'il était possible de résoudre les sudoku par la méthode du backtracking. J'ai d'abord pensé que l'exécution serait extrêmement longue mais le texte précisait que quelques secondes suffisaient avec un langage compilé sur une machine assez puissante. Pour le vérifier, j'ai programmé l'algorithme et j'ai constaté que l'exécution était bien plus rapide que le texte ne le disait : il faut moins d'une seconde à CAML, qui est un langage interprété, pour résoudre les grilles sur mon PC, qui date pourtant de 2003.
Conclusion
J'ai apprécié de travailler sur ce sujet car le sudoku est un jeu aujourd'hui très connu et également très simple à comprendre. La programmation était aussi agréable puisqu'il s'agissait de faire faire à l'ordinateur des actions assez répétitives auxquelles j'étais déjà habitué. J'ai donc réfléchi pendant deux semaines sans rien écrire, afin de construire l'algorithme dans ma tête et de le programmer en seulement une heure et demi. J'ai procédé de la même manière pour le second.
Notes diverses
Formule magique
k=(r-(r mod n ))×n2+(r mod n)×n+j+(n2×i)
Théorème : Lorsque (i,j) décrit [1,n]2, k décrit la liste des cases de la région r.
Démonstration : On numérote les régions de 0 à n2.
On cherche d'abord à se placer dans la case en haut à gauche de la région r.
(r mod n)×n désigne la colonne recherchée. En effet, la région r comportant n×n cases, il y a n×n régions dans la grille, réparties en n lignes de n régions. La région r est donc la région n° (r mod n) de sa ligne de régions. Multiplier par n donne alors clairement le numéro de la première colonne de la région.
(r-(r mod n))×n2 désigne la ligne recherchée. En effet, on a vu que la région r est la région n° (r mod n) de sa ligne de régions. (r-(r mod n)) est donc le numéro de la première région de la ligne de régions de r, qui est aussi le nombre de lignes au-dessus de la région r. Ces lignes comportant chacune n2 cases, la première case de r est bien k.
Ajouter j permet de se déplacer sur une ligne.
Ajouter n2×i permet de se déplacer sur une colonne.
Notations et constantes
Construire les 9 régions sans tenir compte des lignes et colonnes laisse : (9!)9=1,09×1050 possibilités.
Le nombre de grilles différentes (d'après Bertram Felgenhauer et Frazer Jarvis) est : 9!×722×27×27 704 267 971=6,67×1021.
Le nombre de grilles différentes (en tenant compte des symétries, d'après Frazer Jarvis et Ed Russell) est : 5 472 730 538.
Extra
Je rajoute ici une fonction qui ne sert pas à la résolution des sudoku mais qui peut se révéler utile à ceux qui s'intéresseraient à cette problématique.
Son rôle est de vérifier l'exactitude d'une grille déjà remplie. On suppose que la grille est de type « int vect vect », c'est-à-dire 9 vect (lignes) de 9 int (colonnes).
Pour chaque ligne, colonne et région, le programme calcule le produit des nombres premiers correspondants (1 est associé au nombre premier 2, 2 au nombre premier 3, 3 au nombre premier 5, 4 au nombre premier 7 et ainsi de suite jusqu'à 9, associé au nombre premier 23). La décomposition en produit de facteurs premiers étant unique (à l'ordre près), le produit obtenu sera égal à 223092870 si et seulement si la zone considée est composée exactement des chiffres de 1 à 9.
Mon programme de recherche des anagrammes utilise le même principe, cette fois avec les lettres des mots.
let verifie sudoku = let premiers=[|2;3;5;7;11;13;17;19;23|] in let produit=ref 1 in try for i=0 to 8 do for j=0 to 8 do produit:=!produit*premiers.((sudoku.(i).(j))-1); done; if !produit != 223092870 then raise Exit else produit:=1; done; for i=0 to 8 do for j=0 to 8 do produit:=!produit*premiers.((sudoku.(j).(i))-1); done; if !produit != 223092870 then raise Exit else produit:=1; done; for i=0 to 8 do for j=0 to 2 do for k=0 to 2 do produit:=!produit*premiers.((sudoku.(j+i-(i mod 3)).(k+3*(i mod 3)))-1); done;done; if !produit != 223092870 then raise Exit else produit:=1; done; 1;with Exit -> 0;; (*exemple : grille correcte*) verifie [| [|5;2;1;4;7;9;3;8;6|]; [|8;6;7;5;2;3;9;1;4|]; [|3;4;9;6;1;8;7;5;2|]; [|7;9;3;8;5;6;2;4;1|]; [|6;8;4;2;9;1;5;3;7|]; [|1;5;2;3;4;7;8;6;9|]; [|9;1;5;7;3;4;6;2;8|]; [|2;7;8;1;6;5;4;9;3|]; [|4;3;6;9;8;2;1;7;5|]|];; (*exemple : grille incorrecte*) verifie [| [|5;2;1;4;7;9;3;8;6|]; [|8;6;7;5;2;3;9;1;4|]; [|3;4;9;6;1;8;7;5;2|]; [|7;9;3;8;5;6;2;4;1|]; [|6;8;4;2;2;1;5;3;7|]; [|1;5;2;3;4;7;8;6;9|]; [|9;1;5;7;3;4;6;2;8|]; [|2;7;8;1;6;5;4;9;3|]; [|4;3;6;9;8;2;1;7;5|]|];;
Bibliographie et sources
- Article Évaluer la difficulté d'une grille de sudoku à l'aide d'un modèle contraintes de Narendra Jussien, de l'école des Mines de Nantes.
- Article sudoku de Wikipédia
- Page de Gordon Royle sur le sudoku
- Page de Gary McGuire sur le sudoku
Cette page en français a été créée par Peter à partir de connaissances ou expériences personnelles et d'un exposé scolaire, 29 avril 2006 et modifiée pour la dernière fois 25 août 2020. Son avancement est noté 3/3.