Algorithmes de tri
Une comparaison entre différents algorithmes de tri (sélection, insertion, bulle, fusion) écrits en C.
- Parenté :
- Programmation
- Algorithmes de tri
Introduction
Les fonctions réalisées ont pour but de trier des tableaux de nombres, du type T_Elt. Ces tableaux n'ont pas de taille maximale imposée a priori.
Les fonctions de tri prendront donc en argument d'une part le tableau à trier et d'autre part sa taille.
Afin de pouvoir tester les différentes fonctions, les comparaisons et affectations que chaque méthode de tri produit dans les tableau sont comptabilisées dans une variable globale nommée resultat. Ces comptages sont ici commentés pour que les fonctions puissent être testées avec l'algorithme présenté en cinquième partie.
Fichier Tris.h :
#include <time.h>
typedef int T_Elt;
typedef struct
{
unsigned long long nbComparaisons;
unsigned long long nbAffectations;
clock_t duree_en_clock_t;
} T_Res;
Tri par sélection
Cette méthode cherche le plus petit élément du tableau et l'échange avec le premier élément. Elle cherche ensuite le second plus petit et l'échange avec le second élément du tableau, et ainsi de suite jusqu'à la fin du tableau.
On peut observer que le traitement tel qu'implémenté ci-dessous nécessite deux boucles for imbriquées dont l'ordre de grandeur du nombre d'itérations est n. On a donc un algorithme en O(n²).
void Tri_Selection (T_Elt T[], int n)
{
int i, j, c, p;
for(i=0;i<n;i++){ //on parcourt le tableau
p=i;
for(j=i;j<n;j++){ //on cherche la position p du plus petit élément
if(T[j]<T[p]) p=j;
//resultat.nbComparaisons++; //comptage des opérations
}
c=T[i]; //on échange
T[i]=T[p]; //les deux
T[p]=c; //nombres
//resultat.nbAffectations+=2; //comptage des opérations
}
}
Tri par insertion
Ce tri parcourt le tableau et, pour chaque élément rencontré, recherche la position à lui affecter. Cette position est définie comme étant juste avant le premier élément rencontré qui soit supérieur à celui en cours.
Une fois cette position trouvée, tous les nombres se trouvant entre la position initiale de l'élément et sa position finale sont déplacés pour pouvoir enfin écrire l'élément à sa place.
Comme précédemment, la complexité est en O(n²).
void Tri_Insertion (T_Elt T[], int n)
{
int i, k, c, p;
for(i=1;i<n;i++){
c=T[i];
p=0;
while(T[p]<c){ //on cherche la position p à affecter à l'élément
p++;
//resultat.nbComparaisons++; //comptage des opérations
}
for(k=i-1;k>=p;k--){ //on décale les nombres
T[k+1]=T[k];
//resultat.nbAffectations++; //comptage des opérations
}
T[p]=c; //on écrit l'élément
//resultat.nbAffectations++; //comptage des opérations
}
}
Tri bulle
Ce tri cherche des suites de deux éléments consécutifs dont le premier est supérieur au second. Tant que l'on trouve de telles séquences, on échange les deux éléments.
Cet algorithme fonctionne en O(n²), sauf lorsque le tableau est déjà trié (O(n) dans ce cas).
void Tri_Bulles (T_Elt T[], int n)
{
int flag, i, c;
flag=1;
while(flag){ //tant qu'on modifie le tableau
flag=0;
i=0;
while(i<n-1){
if(T[i]>T[i+1]){ //si élément est supérieur au suivant
c=T[i]; //on échange
T[i]=T[i+1]; //les deux
T[i+1]=c; //nombres
flag=1;
//resultat.nbAffectations+=2; //comptage des opérations
}
i++;
//resultat.nbComparaisons++; //comptage des opérations
}
}
}
Tri fusion
Le tri fusion est beaucoup plus performant que les tris précédents. Il ne consiste pas réellement à trier des valeurs, mais à fusionner des listes triées. Pour cela, le tableau est découpé récursivement en une série de listes, de taille 1. Ces listes d'un élément sont ainsi triées. On fusionne ensuite progressivement les listes contiguës pour finalement avoir un tableau complètement trié.
Le découpage récursif se fait grâce à la fonction tri_par_fusion et la fusion des listes triées grâce à la fonction fusionner.
void Tri_Fusion(T_Elt T[], int n)
{
tri_par_fusion(T, 0, n-1);
}
void tri_par_fusion(T_Elt t [], int a, int b){ //découpage récursif
int m;
if (a < b){
m = (a + b)/2;
tri_par_fusion(t, a, m);
tri_par_fusion(t, m+1, b);
fusionner(t, a, m, b);
}
}
void fusionner(T_Elt T[], int a, int m, int b)
{
int i, j, k, n;
n=m-a+1; //n : nombre d'éléments de la première partition
int save[n];
for(i=0;i<n;i++){ //on recopie la première partition en mémoire
save[i]=T[a+i];
}
i=a; //i décrit le tableau
j=0; //j décrit la sauvegarde de la première partition
k=m+1; //k décrit la seconde partition
while(j<n){ //tant qu'il reste des éléments dans la première partition
if(k<=b && T[k]<save[j]){ //s'il y en a des plus petits
//dans la seconde
T[i]=T[k];k++; //on les écrit
}
else{
T[i]=save[j];j++; //sinon, on recopie la première partition
}
i++;
//resultat.nbComparaisons++; //comptage des opérations
//resultat.nbAffectations++; //comptage des opérations
}
}
Comparaison des quatre méthodes
On teste les tris avec le programme suivant :
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "tris.h"
const int Nb[]= {250000};
void print_table(T_Elt T[], int n){
int i;
for(i=0;i<n;i++){
printf("%d ", T[i]);
}
printf("\n");
}
int main(void)
{
clock_t start, stop;
int i, j, c, n;
// Initialisation du générateur de nombres pseudo-aléatoires
srand(time(NULL));
for(i=0;i<1;i++){
n=Nb[i];
printf("%d\t", n);
T_Elt Table1[n];
T_Elt Table2[n];
T_Elt Table3[n];
T_Elt Table4[n];
for(j=0;j<n;j++){
c=rand() % n;
Table1[j]=c;
Table2[j]=c;
Table3[j]=c;
Table4[j]=c;
}
start = clock();
Tri_Selection(Table1, n);
stop = clock();
printf("%.3f\t", (float)(stop - start)/CLOCKS_PER_SEC);
start = clock();
Tri_Insertion(Table2, n);
stop = clock();
printf("%.3f\t", (float)(stop - start)/CLOCKS_PER_SEC);
start = clock();
Tri_Bulles(Table3, n);
stop = clock();
printf("%.3f\t", (float)(stop - start)/CLOCKS_PER_SEC);
start = clock();
Tri_Fusion(Table4, n);
stop = clock();
printf("%.3f\t", (float)(stop - start)/CLOCKS_PER_SEC);
printf("\n");
}
return 0;
}
| Taille du tableau | Tri par sélection (s) | Tri par insertion (s) | Tri bulle (s) | Tri fusion (s) |
|---|---|---|---|---|
| 1 000 | 0.000 | 0.000 | 0.010 | 0.000 |
| 2 500 | 0.010 | 0.010 | 0.050 | 0.000 |
| 5 000 | 0.060 | 0.050 | 0.190 | 0.000 |
| 7 500 | 0.130 | 0.100 | 0.430 | 0.000 |
| 10 000 | 0.240 | 0.170 | 0.770 | 0.000 |
| 12 500 | 0.360 | 0.280 | 1.210 | 0.010 |
| 15 000 | 0.530 | 0.390 | 1.740 | 0.000 |
| 17 500 | 0.730 | 0.530 | 2.390 | 0.000 |
| 20 000 | 0.940 | 0.710 | 3.110 | 0.010 |
| 22 500 | 1.190 | 0.880 | 3.910 | 0.010 |
| 25 000 | 1.480 | 1.090 | 4.840 | 0.000 |
| 27 500 | 1.780 | 1.320 | 5.860 | 0.000 |
| 30 000 | 2.110 | 1.590 | 6.970 | 0.000 |
On peut ensuite tracer le graphe correspondant dans GnuPlot en utilisant le code suivant :
GNUTERM = "x11" set term png size 800, 600 set output "TestTris.png" set title "Temps d'execution des differents algorithmes" set xlabel "Nombre d'elements" set ylabel "Temps (s)" set key left plot [*:*] [0:7] "Resultat.txt" title "Selection" with linespoints, "Resultat.txt" using 1:3 title "Insertion" with linespoints, "Resultat.txt" using 1:4 title "Bulles" with linespoints, "Resultat.txt" using 1:5 title "Fusion" with linespoints
On obtient alors le résultat :
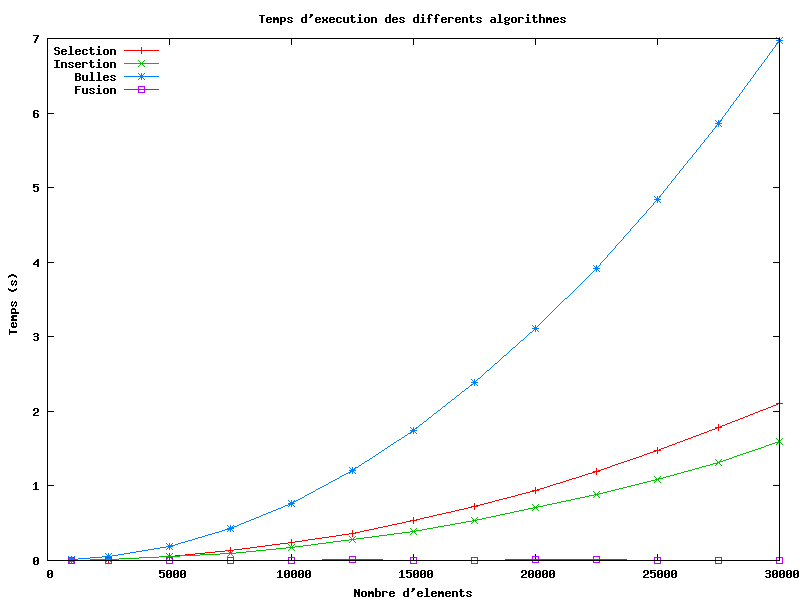
Si l'on compare ces différentes méthodes de tri, on peut s'apercevoir que le tri bulle est le moins efficace en terme de temps d'exécution. Viennent ensuite le tri par sélection puis celui par insertion. La différence est grande entre le tri bulle et ces deux tris. Ainsi, pour trier un tableau de 30000 éléments aléatoires, le tri bulle met trois fois plus de temps que les deux autres.
Cependant, il faut noter que le tri bulle est bien plus performant que les deux autres sur un tableau déjà trié. Ainsi, un autre test, sur un tableau déjà ordonné, avait donné les résultats suivants :
| Taille du tableau déjà trié | Tri par sélection (ms) | Tri par insertion (ms) | Tri bulle (ms) |
|---|---|---|---|
| 25 000 | 1740 | 1110 | 0,0 |
Enfin, l'efficacité du tri fusion est sans commune mesure avec les trois tris « lents » précédents : 60 ms lui suffisent pour trier un tableau de 250 000 éléments !
J'ai testé par curiosité les algorithmes lents sur un tel tableau. Pour le trier, il a fallu plus de :
| Taille du tableau | Tri par sélection | Tri par insertion | Tri bulle |
|---|---|---|---|
| 250 000 | 2 minutes et 25 secondes | 1 minute et 50 secondes | 8 minutes et 10 secondes |
En conclusion, on peut dire que ces trois algorithmes ne conviennent que pour des tableaux courts et sont simples à mettre en place. Le tri fusion (ou un autre tri rapide) est nécessaire dès que les tableaux ont une plus grande taille.
Cette page en français a été créée par Peter à partir de connaissances ou expériences personnelles et d'un exposé scolaire, 17 juin 2008 et modifiée pour la dernière fois 25 août 2020. Son avancement est noté 2/3.